商业经济研究杂志已发表格式范文参考
1.基于多任务学习的通用滤波多载波调制识别与信噪比估计
作者:张天骐,吴云戈,吴仙越,李春运
作者单位:重庆邮电大学
关键词:通用滤波多载波( UFMC);调制识别;信噪比估计;多任务学习;神经网络
摘 要: 非协作通信通用滤波多载波( Universal Filtered Multi-carrier,UFMC) 信号子载波所存在的调 制识别以及信噪比估计问题有待解决,但目前研究只针对于单一任务。对此,提出一种利用多任务 学习框架的神经网络模型,同时解决调制识别以及信噪比估计任务。首先得到 UFMC 系统接收端信 号,求解出信号同相正交分量作为输入特征; 接着在多任务学习框架上构建神经网络,采用的神经网 络是将卷积神经网络与长短时记忆网络串联; 最后利用上述模型对两个任务进行联合求解。实验结 果表明,所构建多任务学习模型性能优于单任务学习,在信噪比为 0 dB 时,子载波调制识别准确率 提升 7. 71%,信噪比估计均方误差减小 45. 6%。
0 引 言
随着通信技术的不断进步,对信号进行调制识 别和信噪比估计逐渐引起人们关注。调制识别广泛 应用于军事和民用领域: 在军事领域,雷达信号调制 识别是电子侦察和电子对抗的重要课题[1]; 在民用 领域,调制识别技术主要用于提高频谱利用率[2]。 信噪比估计在现代无线通信系统中发挥着重要作 用,因为准确的信噪比值有助于在各个方面提高传 输性能。综上所述,在非合作通信系统中,对信号进 行调制识别以及信噪比估计具有重要意义。
目前,已有方法可以实现信号调制识别: 文献 [3]利用指数范数结合决策树分类器进行调制识 别; 文献[4]和文献[5]分别利用卷积神经网络 ( Convolutional Neural Network,CNN) 结合长短时记 忆网络( Long Short Term Memory Network,LSTM) 和 人工神经网络网络进行调制识别,但是未达到完全 识别; 文献[6]利用二维异步同相正交直方图结合 径向基函数神经网络( Radial Basis Function Neural Network,RBFNN) 进行调制识别,但是信噪比低时部 分 QAM 信号效果不理想。
上述识别方法只针对单载波信号,对通用滤波 多载波( Universal Filtered Multi-carrier,UFMC) 信号 子载波进行调制识别还处于初级阶段,但是正交频 分复用( Orthogonal Frequency Division Multiplexing, OFDM) 信号的调制识别已有部分文献成果: 文献 [7]利用四阶时延矩进行调制识别,但是未达到 100%识别; 文献[8]将循环谱作为输入特征,再利 用 CNN 实现对 OFDM 信号的调制识别,但是在信噪 比低的情况下效果不理想; 文献[9]和文献[10]分 别利 用 同 相 正 交 序 列 ( In-phase and Quadrature sequence,I/Q) 结合 CNN 模型对信号进行调制识 别,但是前者只对 4 种信号完成调制识别,后者在低 信噪比情况下效果不佳; 文献[11]利用 CNN 对 OFDM 单-混信号进行调制识别,但是识别阶数较 低。综上,对于 OFDM 信号调制识别已有方法可以 实现,但是随着用户数量爆炸式的增长以及用户对 于多元化应用场景的需求,OFDM 信号逐渐难以满 足用户要求。而 UFMC 对整个频带进行划分,并采 用切比雪夫滤波器在子带上进行滤波处理,能够降 低带外泄露,对比 OFDM 信号更适合应用于低时延 以及短数据包的应用场景中。所以,在 OFDM 信号 调制识别的基础上对 UFMC 信号进行调制识别具 有研究价值。
信噪比估计算法可分为非数据辅助[12]和数据 辅助算法[13]两种。文献[14]采用频域分离噪声的 方法进行信噪比估计; Boumard [15]提出利用前导符 号估计噪声方差,再利用子信道估计系数得到系统 的信噪比。用于对图像进行处理的深度神经网络逐 渐应用于通信信号,Chen 等人[16]提出一种结合深 度学习和协方差矩阵的信噪比估计方法。
在大多数情况下,我们关注的是单个任务的求 解,但是结合现实生活,往往存在多个任务需要共同 解决,因 此 人 们 提 出 了 多 任 务 学 习 ( Multi-Task Learning,MTL) 模型,同时学习多个相关任务,通过 共享模型参数提高整体性能,包括提高泛化准确率、 学习速度等。相比于单任务学习模型( Single-Task Learning,STL) ,MTL 模型性能更加优越,因此已经 应用于多个领域。 本文提出一种基于 MTL 框架,利用 CNN-LSTM 模型同时完成 UFMC 信号子载波调制识别以及信 噪比估计。
本文将信号参数求解中的信噪比估计作 为另一个任务进行求解,主要原因如下: 信噪比可以 表征信道的质量,信噪比参数的获取对通信信号的 解调等起关键作用; 利用本文所构建的神经网络,完 成上述两个任务,可以最大限度地利用网络的性能, 实现任务的同步解决; 利用本文输入特征以及神经 网络难以对其他参数进行求解,需要重新提取特征 以及构建神经网络; 信噪比估计可以被视为参数估 计中的一种,所以本文算法合理。本文求解思路如 下: 首先在接收端对信号进行均衡处理得到 I/Q 序 列,接着搭建 MTL 框架,最后利用 CNN-LSTM 模型 双分支输出层同时实现 UFMC 系统对下 BPSK、 4QAM、8QAM、16QAM、64QAM 5 种信号的调制识别 以及信噪比估计。
1 系统模型与数据集的构造
1. 1 UFMC 系统模型
图 1 为 UFMC 系统的结构。

假设系统总子载波个数为 NB,并且系统将子载 波分配到 B 个子带上,每个子带上的子载波数 M = NB /B。发送端信号的频域用 Si( k) 表示,进行 N 点 快速傅里叶反变换( Inverse Fast Fourier Transform, IFFT) ,得到其时域信号表达式为

式中: Ki 代表的是第 i 个子带上的子载波数。
得到上述时域信号后,对其进行滤波处理,滤波 器采用切比雪夫滤波器。滤波器长度为 L,卷积后 的 UFMC 符号长度可以表示为 N+L-1,卷积后的表 达式为

式中: fi 代表滤波器系数; * 代表线性卷积。
将经过滤波处理后的信号叠加,得到时域传输 信号,因此 UFMC 系统发送端信号表达式为

信号经过信道进行传输时,叠加噪声一起到达 接收端。在实际应用场景下,无线信号在传播过程 中会受到多径效应影响,所以为接近真实场景,本文 采用的是莱斯信道。莱斯信道的具体参数设置为信 道的采样率为 1 MHz,平均路径增益为 0. 5 dB,最 大多普勒频移为 1 Hz,多普勒谱的带宽为 8 Hz。时 域信号表达式为
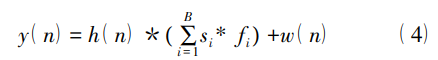
接下来需要对上述信号进行快速傅里叶变换 ( Fast Fourier Transform,FFT) ,此时信号长度大于 N,对时域接收信号进行补零操作使长度变为 2N, 在此基础上完成 FFT 变换。此时输出信号表达 式为

式中: H( k) 代表信道响应的频域信号; Fi ( k) 代表滤 波器系数频域; Si ( k) 代表 si ( n) 的 2N 点 FFT; W( k) 代表高斯白噪声频域。

式中: K'i 代表各子带中的子载波。
根据式( 7) 和式( 8) 可得,公式中不仅含有有用 信息,还包含一些在传输过程中所造成的干扰信息, 因此需要对 Si( k) 的奇数项进行消除,即可得到接 收信号。
1. 2 发送信号恢复
为提高接收信号的可靠性,本文利用迫零均衡 器对接收信号进行处理。
对滤波器进行估计,并且求解出原型滤波器,表 达为

式中: f( k) 代表滤波器估计系数。
对其进行 FFT 变换,表达式为
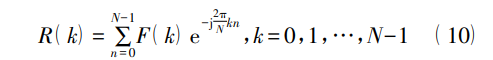
接着求解特定子带原型滤波器的倒数,表达 式为
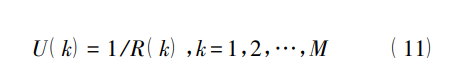
将得到的信号 Si ( k) 重新构建为矩阵形式,并 且得到 U( k) 的矩阵形式 U,两者进行逐元素乘法, 即可得到消除滤波器影响后的信号。
图 2 为进行均衡前后的信号星座图,其中子载波为 4QAM,信噪比为 5 dB。从图中可以看出,未进 行均衡的信号受到的影响比较大,难以分辨调制方 式; 经过迫零均衡后的信号虽然仍受到部分影响,但 是依然可以识别调制方式。

1. 3 输入特征
本文的输入特征是 I/Q 序列,利用在 1. 1 节中 已经获得接收端信号对其进行实虚部分离即可得到 I/Q 分量。文献[7-8]利用四阶时延矩和循环谱进 行特征构造,求解过程相比 I/Q 分量更加繁琐,计算 复杂度高,性能不及本文所提方法。本文利用的输 入特征是 I/Q 分量,不需要进行复杂的变换,直接输 入到神经网络中,能够保留信号的原始信息,从而获 取信号的原始频域特性,可以降低系统的复杂度,取 得较好的分类准确率。
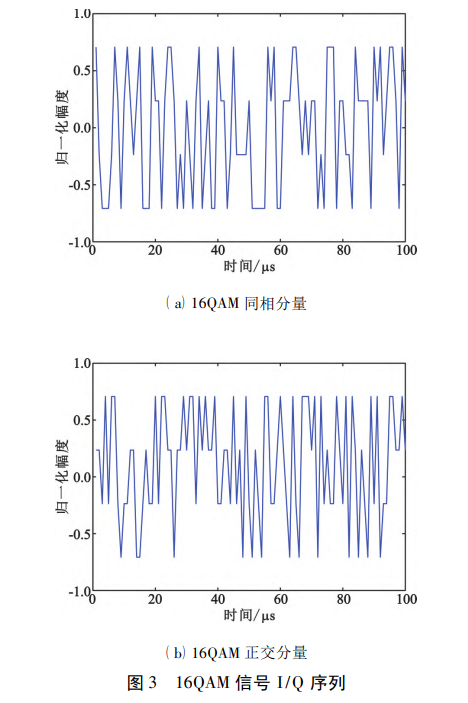
图 3 为 16QAM 信号的可视化图像,可以看出, 16QAM 信号的同相正交分量幅度变化 4 次,因此 I/Q 分量具有良好的特征表达能力,可以从中获取 高维特征信息,求解信号调制方式以及完成信噪比 估计。
1. 4 数据集构造
本小节介绍数据集的构建流程。发送信号生成 之后,经过信道到达接收端,此时利用接收端信号求 解出信号的 I/Q 序列。本文采用的是 UFMC 系统下 的 数 据 集,包 含 BPSK、4QAM、8QAM、16QAM、 64QAM 5 种调制信号。为使数据集中数据包含更 加全面,采用的是多信噪比的形式,信噪比范围是 0~14 dB,间隔为 2 dB,共有 8 种信噪比,在不同信 噪比下对不同的调制信号产生 1 000 个训练样本和 100 个测试样本,总共生成 40 000 条训练数据和 4 000 条测试数据。
2 基于 MTL 模型的联合算法
利用神经网络对多个任务进行分开求解时忽略 多个任务之间的相关性,因此提出利用 MTL 求解 UFMC 系统子载波调制识别以及信噪比估计问题。 本文的 MTL 模型采用硬参数共享方法。本文选用 CNN-LSTM 模块,利用卷积核以及门控机制对输入 信号进行特征提取,获得高维度信息。
模型结构如图 4 所示。为获得较好的性能,本 文将 I/Q 序列构成 2×1 024 的二维数据,作为网络 模块的输入,利用其具有良好的特征表达能力,使本 文算法具有更为优异的性能,同时完成子载波调制 识别以及信噪比估计。

2. 1 特征提取
本文所采用的 CNN-LSTM 网络的特征提取模 块具有 6 个一维卷积层、4 个平均池化层和 2 个 LSTM 层,其中,Fil 表示卷积核个数,Ker 表示卷积 核尺寸。
在 LSTM 模块采取的激活 函 数 是 线 性 整 流 ( Rectified Linear Unit,ReLU) 函数。
2. 2 分类器和预测模块
2. 2. 1 分类器模块
输入数据经过特征提取和特征融合后,通过展 平层( Flatten) 将二维输出压缩为一维特征矢量。分 类器模块由 2 个全连接层( Dense) 、2 个随机失活层 ( Dropout) 以及 1 个输出层组成。全连接层作用是 对调制方式进行分类,并且都使用 ReLU 激活函数。
随机失活层的目的是使神经元按照设置比例停 止工作,以减少模型的过拟合现象。两层随机失活 层的置零比例 rate 分别为 0. 5 和 0. 2。
输出层采用的 Softmax 激活函数能够将第二个 全连接层的输出转换为一个 1×5 维的概率矢量 p = [p1,p2,…,p5],分别代表不同调制方式的概率,最 终通过判定最大值作为调制方式。
利用上述激活函数得到预测标签 yi 后,将其与 真实的标签 yreal i 代入到损失函数中,计算出一个批 次的损失。损失函数表达式为
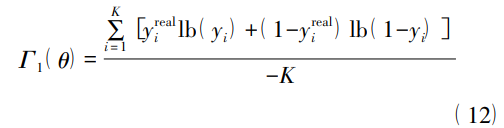
式中: K 代表的是一个批次中包含的样本数。
2. 2. 2 预测模块
预测模块输出层采用的是线性激活,并且利用 均方误差来衡量预测的准确性。对于信噪比估计任 务的损失函数表达式为
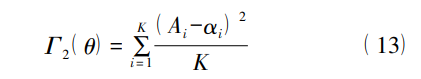
式中: Ai 代表信噪比预测值; αi 为信噪比实际值。 在文献[9]的基础上进行多任务学习。该文献 的损失是直接将两个任务的损失函数进行加和,表 达式为

但是由于不同任务的难易程度不同,难以保证 两个任务同时达到拟合效果。考虑到此问题,本文 采用的是考虑权重优化的多任务学习。本文引入损 失权重 λ1 和 λ2 对两个任务进行损失平衡。对式 ( 14) 进行更新可得表达式为

为了防止整体的损失被一个任务主导,引入损 失权重,取值如公式( 15) 所示,防止整体的损失被 一个任务主导,提高系统的泛化性能,从而在更新公 式的复杂度和性能之间取得平衡。
2. 3 算法步骤
综上所述,对信号提取 I/Q 序列作为输入特征, 构建 MTL 框架结合 CNN-LSTM 模型实现 UFMC 系 统子载波调制识别和信噪比估计,算法实现的步骤 如下:
步骤 1 发送信号通过 UFMC 系统,到达接收 端,接着进行迫零均衡处理,提取 I/Q 序列,构建训 练集和测试集。
步骤 2 搭建 MTL 框架,结合 CNN-LSTM 模 型,利用训练集进行网络训练。
步骤 3 对两个任务进行联合优化处理,保存 性能最好时的模型。
步骤 4 完成以上训练步骤后,将测试集作为 神经网络输入,完成 UFMC 系统子载波的调制识别以及信噪比估计。
3 仿真实验及结果分析
本节使用 MATLAB2018 进行调制信号样本的 仿真,信道设置和 1. 1 节一致,部分参数设置如下: FFT 点数设置为 1 024,子带数量设置为 24,滤波器 长度设置为 43。在 TensorFlow2. 13. 0 版本下构建 MTL 结合 CNN-LSTM 模型,完成训练和测试。
3. 1 UFMC 信号子载波调制识别和信噪比估计性 能分析
本实验验证算法对于 UFMC 信号子载波调制 识别性能以及信噪比估计的有效性。图 5 给出了子 载波调制识别的准确率以及信噪比估计的均方误 差。由图 5( a) 可见,随着信噪比的增加,UFMC 信 号调制识别准确率也在上升,在信噪比大于等于 2 dB 时可以实现 BPSK、4QAM 和 8QAM 信号的完 全识别,在信噪比大于等于 10 dB 时能够实现所有 子载波的调制识别。从图 5( b) 可以看出,在信噪比 较低的情况下,信噪比的均方误差较大,但是随着信 噪比的升高,估计的均方误差整体呈下降的趋势,并 且整体误差小于 1。

3. 2 STL 与 MTL 模型性能对比
本实验对比 STL 与 MTL 模型的性能。STL 和 MTL 模型具有相同的数据集与神经网络模块。从 图 6( a) 可以看出,STL 模型识别准确率随着信噪比 增加也在上升,但是未达到 100%识别; MTL 模型相 比于 STL 模型,在信噪比等于 10 dB 时准确率提升 1. 8%。从图 6( b) 中可以得出,随着信噪比的增加, 两者对于信噪比估计的均方误差都呈下降趋势,但 是 STL 模型的误差要高于 MTL 模型。综上所述, MTL 模型的性能更好,通过联合学习多任务正则化 模型对信息进行共享和补充,增强模型预测准确性 和调制识别的泛化能力。
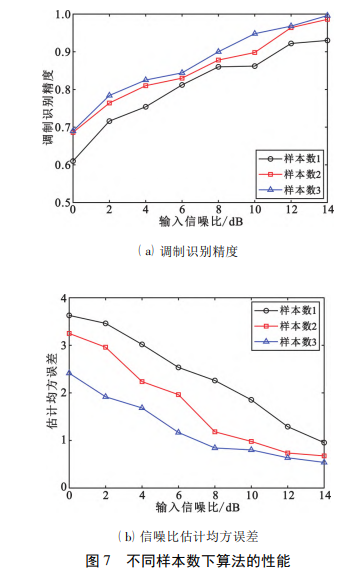
3. 3 样本数对所提算法性能影响
本实验验证不同样本数对模型性能的影响,通 过改变样本数对算法性能进行测试。图 7 给出不同 样本数对识别精度的影响,其中样本数 1、2、3 分别 代表样本数为 12 000、20 000、28 000。从图 7 可 知,随着样本数量的增加,调制识别和信噪比估计的 性能也在提升。由此可知,在进行神经网络训练时,需要充足的样本数来提升网络的泛化能力。

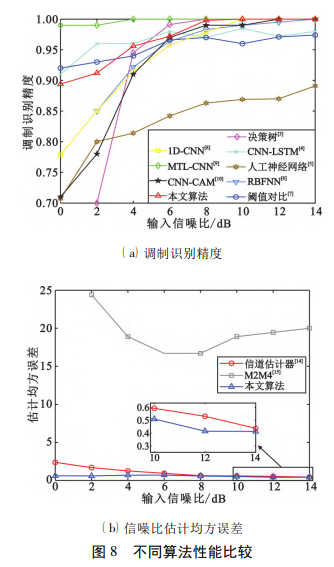
3. 4 不同算法性能对比
本实验验证不同算法下的性能。从图 8( a) 可 以看出,文献[3]利用指数范数结合决策树,在信噪 比大于等于 8 dB 时完成对所有信号的调制识别,但 是需要利用 2 个特征参数以及 4 个门限值,并且门 限值需要进行多次实验进行求解,所需要的时间成 本较高; 文献[4]利用 CNN-LSTM 网络进行调制识 别,但是在信噪比等于 14 dB 时未能实现 100%识 别; 文献[5]利用人工神经网络进行调制识别,但是 由于输入是原始信号,未做任何处理,调制识别不 佳,在信噪比等于 14 dB 时准确率低于 90%; 文献 [6]利用二维异步同相正交直方图结合 RBFNN 进 行调制识别,但是由于高阶 QAM 易受到噪声影响, 所以在信噪比低时部分 QAM 信号识别效果不佳; 文献[7]和文献[9]对 OFDM 信号进行调制识别,前 者利用四阶时延矩的理论值和方差,设置阈值,对子 载波进行调制识别,在信噪比大于等于 8 dB 时完成 对所有子载波的调制识别,后者利用 CNN 结合 I/Q 分量,获得较好的性能,但是两者的调制阶数最高只 有 16 阶; 文献[8]和文献[10]利用 CNN,将循环谱 作为特征,但是未进行降噪处理,所以性能不及本 文。图 8( b) 对比了不同算法下的信噪比估计值的 均方误差,从图中可以看出文献[14]和文献[15]分 别 利 用 二 阶 四 阶 矩 ( Second and Fourth Order Moments,M2M4) 算法以及信道估计器对信噪比进 行估计,性能受到信道变化和噪声方差影响,所以估 计均方误差大于本文。本文利用 MTL 结合 CNNLSTM 模型,减少过拟合现象,从而提升了算法性 能。综上所述,本文所提算法性能优于对比方法。
4 结束语
目前对于 UFMC 系统子载波调制识别以及信 噪比估计问题涉及较少。针对以上问题,本文构建 MTL 框架结合 CNN-LSTM 模型进行同步求解,为后 续信号的调制解调起重要作用。首先构建 UFMC 模型,得到接收端信号,接着求解信号的 I/Q 分量, 最后构建 MTL 框架对两个任务进行同时求解。由 于本文采用 MTL 框架,通过挖掘任务之间的关系, 能够得到额外的有用信息,增加模型的鲁棒性,提升 两个任务的性能,效果优于 STL 模型。实验结果表明,整体的信噪比估计均方误差小于 1,在信噪比大 于等于 10 dB 时能完成对所有子载波识别,并且性 能优于本文所列举的其他方法。但是,本文针对的 是低阶调制信号,下一步将考虑提升调制信号阶数 进行预测和分类。
